Velocity and relative velocity are two concepts in physics that are often confused with each other. While they both relate to the movement of objects, they have distinct differences in their definitions, calculations, and real-world applications.
When we talk about the motion of objects, velocity is an important concept that comes into play. This is the measurement of speed and direction. There is another concept related to velocity that is often confused with it – relative velocity. This article will clarify any confusion that you may have about the differences between relative and absolute velocity.
Physics is a branch of science that deals with energy, matter, and their interactions. It has numerous concepts and terminologies that can be confusing to the uninitiated. Two such concepts are velocity and relative velocity. These terms are frequently used in physics and engineering. In this article, we will discuss the Differences Between Velocity and Relative Velocity comparison charts, explaining their meanings, formulas, and applications.
Let’s know about the Velocity
The velocity can be measured by the change of position an object undergoes over time. It’s often measured by the time itself. Simply stated, velocity measures how quickly something moves in any given direction.
Velocity can be used to measure the rate of change in position that an object makes over time. It measures both its speed and direction. Simply stated, velocity measures how quickly something is traveling along its intended course.
Definition of Velocity
The rate at which an object changes position in time is called its velocity. It can also be referred to as its speed or direction. Velocity is also a vector quantity, as the magnitude (speed), and direction (velocity) of velocity are different.
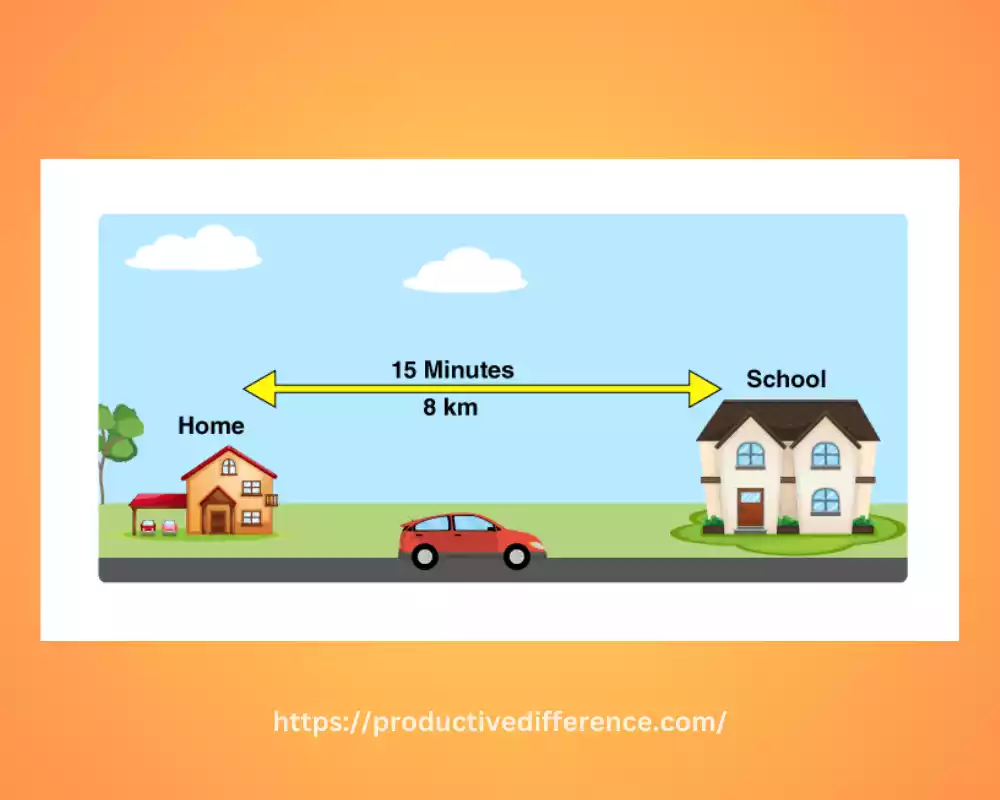
Velocity can be calculated by dividing an object’s displacement by how quickly its travel covers that distance or direction between initial and final positions, in units of time. The displacement is the distance from the initial to the final position.
The definition of velocity can be expressed as:
Velocity (v) = Displacement (Δx) / Time (Δt)
Units for Velocity: The velocity units are usually expressed in terms of distance per time. For example, meters per second (m/s), or kilometers per hour.
The Formula for Calculating Velocity
The formula for Calculating Velocity
Velocity = Distance/ Time
The displacement is the change of position in time. It’s usually measured in meters/second (m/s) or kilometers/hour.
Calculating velocity requires knowing both how quickly an object changes its displacement and when this change occurred; for instance, if an object covers 20 meters in 5 seconds then its velocity would be calculated as follows.
Velocity (v) = 20 meters per five seconds (4 meters/second).
Instantaneous vs. Average Velocity
There are two types of velocity that we can talk about average velocity and instantaneous speed. While they both describe an object’s motion, they are calculated and measured differently.
- Instantaneous Velocity: The instantaneous speed is the object’s velocity at any given moment. It is the velocity of an object at a given instant, such as the velocity of a car at a specific moment during a trip. In order to calculate instantaneous speed, we must know both the position of the object at the exact moment in time and its direction of movement. This can be achieved by calculating the derivative of the object’s position function concerning time.
For example, imagine a car moving at a constant velocity of 60 miles per hour (mph). At any given instant, its instantaneous velocity would also be 60 mph. However, if the car slows down or speeds up, its instantaneous velocity will change accordingly.
- Average Velocity: The average velocity describes the overall speed of an object over a certain period. Calculated by dividing total displacement by the time required to cover the displacement. Average velocity provides a more general idea of how an object moves over a certain distance.
For instance, let’s say a person walks 5 kilometers in 1 hour. Their average velocity would be 5 kilometers per hour (km/h). This doesn’t mean that they walked at a constant velocity the entire time, as their velocity could have changed during their walk.
It’s important to note that instantaneous velocity and average velocity can be different. For example, if a car starts from rest and accelerates to a velocity of 60 mph in 10 seconds, its average velocity during that period would be 6 mph. However, its instantaneous velocity at the end of the 10 seconds would be 60 mph.
Applications of Velocity
The concept of velocity is a key one in physics and has many practical applications. Here are some examples of how velocity is applied in different fields.
Velocity and Physics
In physics, velocity is an important concept, as it helps us describe the motion of objects. The velocity of an object allows us to predict its position in the future and determine its location.
Velocity plays an essential role in many areas of physics such as thermodynamics and electromagnetism, mechanics, and thermodynamics. Mechanically speaking, velocity helps determine an object’s kinetic energy or movement-associated energy while thermodynamically it determines gas molecule distribution within containers. This is crucial in understanding heat transfer, and other thermodynamic processes.
In physics velocity is an important concept to describe motion. There are two types of velocity: uniformed and non-uniform.
- Uniform Velocity: Uniform Velocity is the speed and direction of an object that does not change with time. On a graph of velocity versus time, this is usually represented by a line.
- Non-Uniform Velocity: Non-uniform velocity is the change in the speed or direction of an object over time. A curved line is usually used to represent this on a graph of velocity vs. timing.
Velocity in Engineering
In engineering, velocity is also used to describe fluid motion and sound.
- Fluid velocity: In fluid dynamics, the velocity describes how fast a fluid flows through a channel or pipe. It’s usually measured in feet per second or meters per second.
- Sound velocity: In acoustics velocity is the rate at which sound moves through a material. At room temperature, the velocity of air sound is 343 meters/second (m/s).
Velocity in Sports
In sports, velocity is used as a way to measure the speed of athletes.
- Running Velocity: In running, the velocity of a runner is described. The speed is usually measured in kilometers per hour or meters per second.
- Speed: The speed of a swimmer can be measured by kilometers per hour, meters per second, or even improved stroke technique.
- Strengthening and endurance are also important.
- Velocity for Cycling In cycling, the velocity used is to describe how fast a cyclist travels. It’s usually measured in miles per hour or kilometers per hour. By improving pedaling techniques and increasing power output as well as reducing wind resistance, cyclists can improve their speed.
Velocity in Business
In business, velocity is a key concept. It is used to describe how fast money flows through an economy.
- Velocity in Money: The money’s velocity is an indicator of the speed at which money moves in an economy. Calculated by multiplying the amount of currency in circulation by the number of total transactions. Higher money velocity indicates an active economy. Lower money velocity indicates a slow economy.
Velocity in Technology
In technology, the concept of velocity is used more and more to describe how fast data is transmitted through computers.
- Velocity of Data: Velocity of data measures how fast data can be processed by a computer. In fields like big data analytics where speed is important, it’s becoming more and more relevant.
The concept of velocity has many uses in sports, technology, engineering, physics, and business. Understanding what velocity is, how to calculate it, and the importance of this concept in different areas can allow us to better comprehend the world.
Velocity in Transportation
Transportation industry companies use velocity to measure vehicle speed and time of arrival. Airlines rely on velocity calculations when planning trips between cities while car makers utilize it when testing safety features on new models.
Velocity in Weather Forecasting
Meteorologists measure the velocity of storms, hurricanes, and other extreme weather events, such as tornados. By measuring their velocity, meteorologists can accurately predict their path and intensity and issue timely warnings or plans for emergencies.
Velocity in Motion and Kinematics
Velocity is an essential concept when studying motion and kinematics, providing us with an analysis of object movements through space and time. Sports teams utilize velocity as a way of measuring player speed – measuring it accurately can often decide the outcome of games!
Example
Suppose a ball is thrown straight upward with an initial velocity of 20 meters per second (m/s) from ground level. Neglecting air resistance, what will be the ball’s velocity when it reaches its maximum height?
To solve this problem, we need to use the equations of motion for uniform acceleration. The acceleration of the ball is due to gravity and is approximately equal to -9.8 meters per second squared (m/s^2) on Earth.
The first equation of motion relates the displacement, velocity, acceleration, and time for an object moving with uniform acceleration:
Displacement = Initial Velocity x Time + 0.5 x Acceleration x Time^2
In this case, we know that the ball starts at ground level, so the initial displacement is zero. We also know the initial velocity and acceleration, but we don’t know the time it takes for the ball to reach its maximum height. However, we do know that at the maximum height, the velocity of the ball is zero. So we can use the second equation of motion, which relates the final velocity, initial velocity, acceleration, and displacement:
Final Velocity^2 = Initial Velocity^2 + 2 x Acceleration x Displacement
Since the final velocity is zero at the maximum height, we can solve for the displacement:
Displacement = (Final Velocity^2 – Initial Velocity^2) / (2 x Acceleration)
Displacement = (0 – 20^2) / (2 x -9.8)
Displacement = 20.41 meters
Now we can use the first equation of motion to solve for the time it takes for the ball to reach its maximum height:
20.41 = 20 x Time + 0.5 x -9.8 x Time^2
Simplifying and solving for Time, we get:
Time = 2.04 seconds
Finally, we can use the first equation of motion again to find the velocity of the ball at its maximum height:
Velocity = Initial Velocity + Acceleration x Time
Velocity = 20 + (-9.8) x 2.04
Velocity = 0 meters per second
Therefore, the ball’s velocity when it reaches its maximum height is zero.
The Relationship Between Relative Velocity and Time
We encounter motion every day. Whether we’re walking down the street, riding in a car, or watching a bird fly overhead, we’re experiencing motion. But what exactly is motion, and how can we describe it? To answer these questions we will need to examine some key concepts such as relative velocity and the concept of time.
The Relationship Between Relative Velocity and Time
Relative velocity refers to an object’s velocity relative to another, in other words, measured from their respective perspectives. Time refers to how long an event takes to occur between events – when we discuss relative velocity/time relationships we essentially want to know how long one object takes relative to another one to move a specific distance relative to them.
Formula to express the relationship between velocity and time
d = v × t
The distance between objects is d. v represents the relative speed of the two. t is the amount of time that it takes to cover the distance This formula tells us that the distance between two objects is directly proportional to the relative velocity and time.
Factors Affecting Relative Velocity and Time
Several factors can affect the relationship between relative velocity and time.
These include:
- The Speed of the Objects: The speed of the objects in motion can affect the relationship between relative velocity and time. The time taken for an object to travel a distance is shorter when it moves at a high speed than if it were traveling at a lower speed. This means that the relative velocity will be higher when the objects are moving faster.
- The Direction of Motion: The direction of motion can also affect the relationship between relative velocity and time. When two objects move in the opposite direction from each other, they will have a lower relative speed. This is because the objects are moving towards each other, which means they are covering less distance over time.
- The Distance between Objects: The distance between objects can also affect the relationship between relative velocity and time. As distance increases between objects, time will take for one of them to travel in its entirety. This means that the relative velocity will be lower when the objects are further apart.
Relative Velocity: Everything You Need to Know
Relative velocity has long held an interest for physicists and mathematicians. The concept entails studying an object’s motion relative to another object or frame of reference and has applications across various fields including astronomy, engineering, and physics – among others. Understanding relative velocity is integral for understanding how objects move across space and time.
What is Relative Velocity?
Relative velocity can be defined as the speed of an object, particle, or frame about another object. It is, in simpler words, the relative velocity of an object concerning another object or frame of reference. Calculated by finding the differences between the speeds of two objects.
How Does Relative Velocity Work?
To understand how relative velocity works, let’s consider an example. Imagine two cars driving next to each other on a highway. The first car travels at 60 mph while the second one is at 50 mph. From the perspective of the first car, the second car is moving at a speed of 10 mph. From the perspective of the second car, the first car is moving at a speed of 10 mph in the opposite direction.
This example illustrates how relative velocity works. The velocity of an object is relative to the observer or frame of reference. In this case, the observer is the driver of each car. From their respective points of view, they perceive the motion of the other car differently.
Applications of Relative Velocity
Relative velocity has numerous real-world applications.
Here are some of the most common ones:
- Astronomy: Astronomers use relative velocity to study the motion of celestial bodies. By analyzing the relative velocities of stars and planets, astronomers can determine their trajectories and predict their movements.
- Navigation: Navigation systems, such as GPS, rely on relative velocity to provide accurate directions. By measuring the velocity of a moving object concerning the stationary GPS satellites, the system can calculate the object’s location and provide directions accordingly.
- Engineering: Engineers use relative velocity to design machines and vehicles that can operate efficiently and safely. By understanding how different parts of a machine move concerning each other, engineers can design systems that work together seamlessly.
Relative Velocity in One Dimension
Relative velocity can also be studied in one dimension. In this case, the velocity of the object is measured concerning a single point of reference. The formula for relative velocity in one dimension is as follows:
v(A/B) = v(A) – v(B)
Where v(A/B), is the relative speed of object A concerning object B. v(A), is the velocity for object A. v (B), is the value of the velocity for object B.
Differences between Velocity and Relative Velocity
There are several key differences between velocity and relative velocity.
- Velocity refers to an object’s speed and direction in a straight line, while relative velocity measures its velocity relative to another object.
- Velocity is an absolute measure, whereas relative velocity is a relative measure.
- Velocity is always positive or zero, whereas relative velocity can be positive, negative, or zero.
- Velocity is a scalar quantity, whereas relative velocity is a vector quantity.
Comparison chart between Velocity and Relative Velocity
| Velocity | Relative Velocity |
|---|---|
| Velocity refers to the speed and direction of an object in a straight line. | The relative velocity is the speed of an object toward another object. |
| Velocity is an absolute measure. | Relative velocity is a relative measure. |
| Velocity is always positive or zero. | Relative velocity can be positive, negative, or zero. |
| Velocity is a scalar quantity. | Relative velocity is a vector quantity. |
| Velocity can be measured using methods such as using a speedometer or a radar gun. | Relative velocity can be measured by comparing the velocities of two objects. |
| Velocity is used to calculate the trajectory of a projectile and study the flow of fluids. | Relative velocity is used to determine if two objects are on a collision course and in navigation systems. |
Example 1: Velocity
Imagine a car traveling in a straight line at a constant 50 km/h. We can calculate the car’s velocity by dividing the distance it covers by the time it takes to cover that distance.
If the car travels a distance of 200 km in 4 hours, then its velocity will be:
Velocity (v) = Distance (d) / Time (t)
v = d / t
v = 200 km / 4 hours
v = 50 km/h
So, the car’s velocity is 50 km/h, which is a scalar quantity and always positive.
Example 2: Relative Velocity
Let’s say two people, Alex and Bob, are walking towards each other on a straight road. Alex walks north at 5 km/h while Bob walks south at 3 km/h.
To calculate the relative velocity of Alex concerning Bob, we need to subtract Bob’s velocity from Alex’s velocity.
Relative Velocity (v<sub>AB</sub>) = Velocity of Object A (v<sub>A</sub>) – Velocity of Object B (v<sub>B</sub>)
v<sub>AB</sub> = v<sub>A</sub> – v<sub>B</sub>
v<sub>AB</sub> = 5 km/h – (-3 km/h)
v<sub>AB</sub> = 8 km/h
So, the relative velocity of Alex concerning Bob is 8 km/h, which is a vector quantity and can be positive, negative, or zero.
How Velocity and Relative Velocity are Used in Real Life
- To avoid colliding with other aircraft, pilots must understand relative and absolute velocity.
- The engineers of automobiles use relative and absolute velocity to create cars that are efficient and safe. They must know how the relative and different speeds will affect a car’s safety.
- Astronomers can use relative and absolute velocity to study the motion of stars and planets. Astronomers need to know how fast objects move to predict their movements and calculate their orbits.
- Athletes measure their performance using velocity in various sports. Sprinters will measure velocity to improve running speed, while swimmers will measure velocity to improve lap times.
Applications of Velocity and Relative Velocity
Velocity and relative velocity have many applications in physics, such as:
- Projectile motion: Velocity is used to calculate the trajectory of a projectile, such as a baseball or a bullet.
- Collision detection: Relative velocity is used to determine if two objects are on a collision course.
- Navigation: Velocity and relative velocity are used in navigation systems, such as GPS, to determine the position and speed of an object.
- Fluid dynamics: Velocity and relative velocity are used to study the flow of fluids, such as air and water.
Final words
Velocity and relative velocity are fundamental concepts in physics that are often confused as being synonymous. Velocity refers to the speed and direction of an object traveling along a straight line; relative velocity refers to their relative movement relative to another object.
Velocity measures absolute speeds within straight lines while relativity refers to relative measures between objects (positive/zero/neutral or zero/positive versus vector quantities like speed vs velocity etc), so understanding these distinctions are vitally important when applying physical principles such as navigation or fluid dynamics! Understanding these distinctions is vital when applied in different applications like navigation or fluid dynamics!


