Introduction to Angular Acceleration and Centripetal Acceleration
The difference Between Angular Acceleration and Centripetal Acceleration we will know in this article Let’s start the article.
Acceleration is a fundamental concept in physics that describes the rate of change in an object’s velocity. It measures how quickly an object’s speed or direction changes over time. When an object moves in a straight line, acceleration is simply a change in its speed. However, when an object moves in a curved path, a special type of acceleration called centripetal acceleration comes into play.
Centripetal acceleration is the acceleration experienced by an object moving in a circular path. It is directed towards the center of the circle and allows the object to continuously change its direction while maintaining a constant speed. This acceleration keeps the object moving in a curved path instead of flying off in a straight line.
To understand centripetal acceleration, it’s important to distinguish it from linear acceleration. Linear acceleration refers to the change in an object’s linear velocity, which is the rate of change in its linear displacement. It describes how quickly an object’s speed changes in a straight line. On the other hand, centripetal acceleration relates to the change in an object’s velocity in a circular path.
The term “centripetal” comes from Latin and means “center-seeking.” It indicates that centripetal acceleration always points towards the center of the circle. This inward acceleration is necessary to counterbalance the object’s tendency to move in a straight line tangent to the circle. It allows the object to continually change its direction, resulting in circular motion.
Mathematically, centripetal acceleration can be calculated using two different formulas. One formula expresses centripetal acceleration in terms of velocity and radius, while the other uses angular velocity and radius. Both formulas yield the same result.
Understanding acceleration and centripetal acceleration is crucial for various fields of study, such as physics, engineering, and astronomy. These concepts help explain the motion of objects in circular paths, such as planets orbiting the sun, cars turning around curves, or even the swinging motion of a pendulum.
Acceleration is the rate of change in an object’s velocity, and centripetal acceleration specifically refers to the acceleration experienced by an object moving in a circular path. It allows the object to continually change direction while maintaining a constant speed. By studying acceleration and centripetal acceleration, we gain insights into the dynamics of circular motion and its applications in various scientific and practical contexts.
Learn the Difference Between Centripetal and Angular Acceleration
We should first understand the fundamentals of angular and centripetal speed. The angular speed of a rotating body can be described as its angular rate. When a body is moving in a circle, its direction changes constantly.
A body rotating around a fixed point moves at a constant rate. This body’s direction and velocity change as it rotates. This change in speed produces angular or rotational acceleration. The unit of measurement is the radian/second2. The angular acceleration() function can be written using,
= dw/dt
The angular speed is w.
It is true that a body moving in a circle will always try to maintain a constant speed, but this does not mean the velocity of its movement remains constant. The velocity vector (v) also changes as the direction of the body changes. Centripetal Acceleration is the name of this rate at which velocity(v), changes. The acceleration is always towards the centre. Centripetal Acceleration(a) can be expressed as,
a= v2/r
The radius of a circular path is r.
Acceleration angular
In angular motion, a discussion is made about angular acceleration. Angled motion is found in blades on a fan or wheels running. An angle is drawn in a radial direction to represent the motion. This angle has two sides. One moves along with the object, while the other stays still in relation to Earth. Angle displacement is the name of this angle. The rate at which angular movement changes is called angular speed, and the rate that angular motion changes is called angular acceleration.
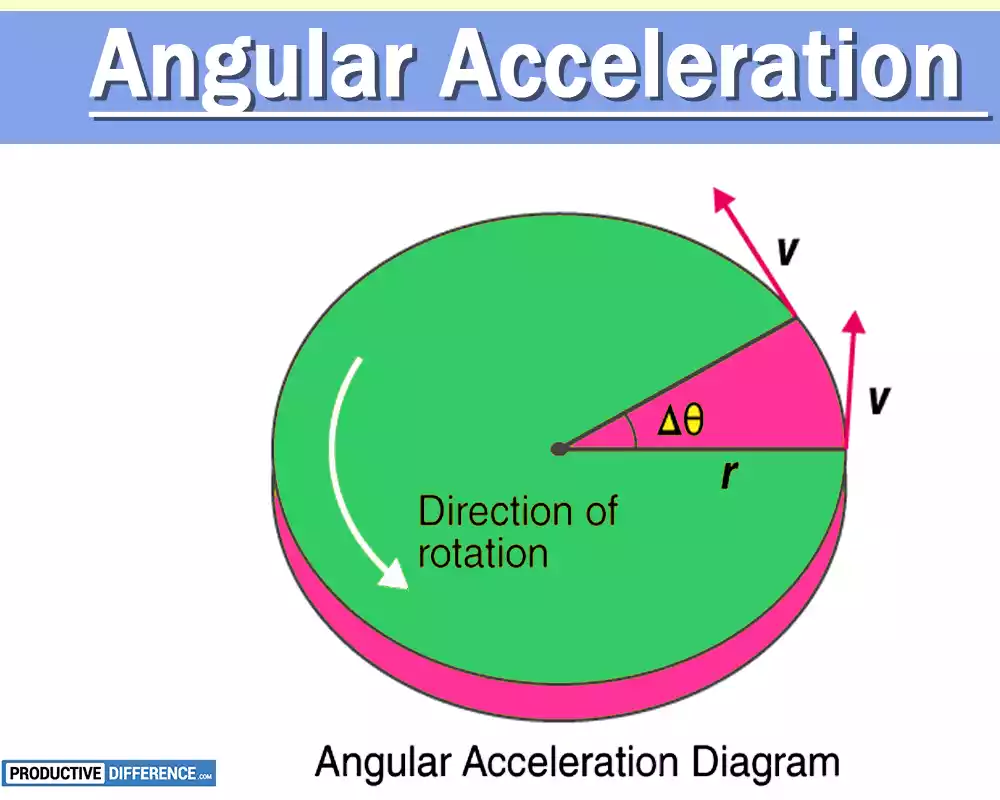
The units are radians/second per second (rad/s 2). The terms angular motion, angular speed, and angular accelerator correspond to the linear motion partner’s displacement, velocity, and acceleration. The vector of angular velocity is the angular acceleration. The axis is the vector. You can use the corkscrew to find out which direction is correct. Imagine that a corkscrew is turned in the same direction as an angular movement.
The direction it “tries” goes, then, represents the direction where the acceleration of the angular motion occurs.
EXAMPLE 1. CALCULATING THE ANGULAR ACCELERATION AND DECELERATION OF A BIKE WHEEL
Suppose a teenager puts her bicycle on its back and starts the rear wheel spinning from rest to a final angular velocity of 250 rpm in 5.00 s. (a) Calculate the angular acceleration in rad/s2. (b) If she now slams on the brakes, causing an angular acceleration of -87.3 rad/s2, how long does it take the wheel to stop?
Strategy for (a)
The angular acceleration can be found directly from its definition in α=ΔωΔt=ΔΔ because the final angular velocity and time are given. We see that Δω is 250 rpm and Δt is 5.00 s.
Solution for (a)
Entering known information into the definition of angular acceleration, we get
α=ΔωΔt=250 rpm5.00 s.=ΔΔ=250 rpm5.00 s.
Because Δω is in revolutions per minute (rpm) and we want the standard units of rad/s2 for angular acceleration, we need to convert Δω from rpm to rad/s:
Δω=250revmin⋅2π radrev⋅1 min60 sec=26.2radsΔ=250revmin⋅2 radrev⋅1 min60 sec=26.2rads
Entering this quantity into the expression for α, we get
α=ΔωΔt=26.2 rad/s5.00 s=5.24 rad/s2.=ΔΔ=26.2 rad/s5.00 s=5.24 rad/s2.
Strategy for (b)
In this part, we know the angular acceleration and the initial angular velocity. We can find the stoppage time by using the definition of angular acceleration and solving for Δt, yielding
Δt=ΔωαΔ=Δ
Solution for (b)
Here the angular velocity decreases from 26.2 rad/s (250 rpm) to zero, so that Δω is –26.2 rad/s, and α is given to be -87.3 rad/s2. Thus,
Δt=−26.2 rad/s−87.3rad/s2=0.300 s.Δ=−26.2 rad/s−87.3rad/s2=0.300 s.
The bicycle would have first accelerated on the ground, then stopped if it had been upside down. It is important to explore the connection between linear and circular motion. It would be helpful to understand the relationship between linear acceleration and angular velocity. As shown in Figure 2, linear acceleration occurs when the circle is tangent at the point where the motion takes place. So, linear acceleration can be called Tangential Acceleration A T.
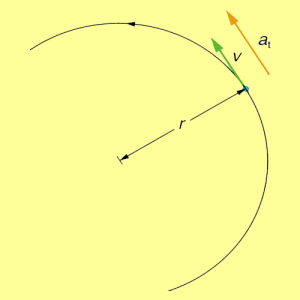
Figure 2. In circular motion, linear acceleration a, occurs as the magnitude of the velocity changes: a is tangent to the motion. In the context of circular motion, linear acceleration is also called tangential acceleration at.
Linear or tangential acceleration refers to changes in the magnitude of velocity but not its direction. We know from Uniform Circular Motion and Gravitation that in circular motion centripetal acceleration, ac, refers to changes in the direction of the velocity but not its magnitude.
An object undergoing circular motion experiences centripetal acceleration, as seen in Figure 3. Thus, at and ac are perpendicular and independent of one another. Tangential acceleration at is directly related to the angular acceleration α and is linked to an increase or decrease in the velocity, but not its direction.
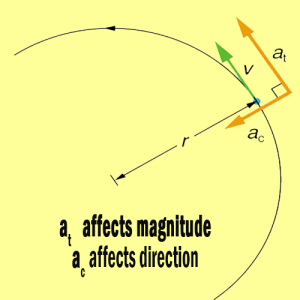
Figure 3. Centripetal acceleration ac occurs as the direction of velocity changes; it is perpendicular to the circular motion. Centripetal and tangential acceleration are thus perpendicular to each other.
Now we can find the exact relationship between linear acceleration at and angular acceleration α. Because linear acceleration is proportional to a change in the magnitude of the velocity, it is defined (as it was in One-Dimensional Kinematics) to be
at=ΔvΔtt=ΔΔ.
For circular motion, note that v = rω, so that
at=Δ(rω)Δtt=Δ(r)Δ.
The radius r is constant for circular motion, and so Δ(rω) = r(Δω). Thus,
at=rΔωΔtt=ΔΔ.
By definition, α=ΔωΔt=ΔΔ. Thus
at = rα,
or
α=atr=t
These equations mean that linear acceleration and angular acceleration are directly proportional. The greater the angular acceleration is, the larger the linear (tangential) acceleration is, and vice versa. For example, the greater the angular acceleration of a car’s drive wheels, the greater the acceleration of the car. The radius also matters. For example, the smaller a wheel, the smaller its linear acceleration for a given angular acceleration α.
Discussion
It takes five seconds to reach a significant angular speed. The angular velocity is negative and large when she brakes. The angle velocity rapidly drops to zero. The relationships in both cases are similar to those of linear motion. When you hit a brick, the velocity changes dramatically in a very short period of time.
Centripetal acceleration
Centripetal acceleration is caused by centripetal forces. The centripetal force keeps objects on a circular path. Centripetal forces always act in the same direction as the center of motion. The Centripetal acceleration is caused by the force. Newton’s 2nd law of motion states that centripetal forces = centripetal speed x mass. Gravitational force is responsible for the centripetal forces required to keep the Earth and Moon in orbit.

Centripetal forces are produced when friction is combined with the normal force of the car’s surface. The centripetal force is directed toward the center of the motion. Therefore, objects try to get close to it. To balance it, a centrifugal torque is required. The linear acceleration of centripetal force is measured by meters per second squared.
Centripetal Acceleration vs Angular Acceleration
1. Centripetal acceleration and angular speed are both vectors.
2. The acceleration of the centripetal force is measured by ms -2 and that of the angular force is measured by rads -2.
3. The centripetal speed is the acceleration in the direction toward the center. This direction varies with the rotation, but the angular speed takes on the direction determined by the law of corkscrews.
4. Centripetal is a line quantity. Angular is an angle quantity.
5. The angular speed of an object rotating with a constant angular rate is 0, while the centripetal velocity has a value equal to radius x angular frequency 2.
We will now look at the comparison chart
| Sr. No. | Acceleration in an angular direction | Acceleration centripetal |
|---|---|---|
| 1 | This is the rate at which the angular speed changes with time. | The acceleration of an object in circular motion is due to the constant change of direction. |
| 2 | The angular acceleration is caused by a change in angular speed of an object. | The continuous changes in direction of the tangential speed of an object is what causes centripetal acceleration. |
| 3 | It is impossible for the direction of the angular acceleration to depend on the location of an object. | The position of the rotating object constantly affects the direction of centripetal accelerating. |
| 4 | The object will either rotate with constant velocity, or not at all. | A zero centripetal speed indicates the object does not move in a circle. |
| 5 | Even with no angular momentum, the object will still be able to rotate. | It is impossible for the centripetal speed of a rotating object to be zero. |
| 6 | The unit of measurement is rad/s2. | The symbol for this is ‘ac or ‘ar and it’s measured in m/s2. |
| 7 | The angular acceleration of a vehicle is determined by a = dodt |
The centripetal force is generated by. ac = v2tr2 = ro22 |
| 8 | The term angular acceleration refers to a motion that is angled. | This is the term for linear motion. |
Differences
Below are the differences and dissimilarities that exist between angular accelerations and centripetal speeds.
- The units are different. Units of centripetal and angular speed are different.
- Centripetal and angular acceleration are related. The former is the rotation of the body about a fixed axis, while the latter is the movement of the body on a circular path.
- The angular acceleration follows a constant direction, i.e. the direction indicated by the corkscrew rules. However, centripetal speed is determined by the path’s center which can change over time.
- Centripetal speed is the linear acceleration derived from angular velocity.
- Centripetal Acceleration a=w 2r
Centripetal and angular acceleration have the same relationship
The expression for centripetal and angular accelerations is different.
You know this,
angular velocity(dw)= angular displacement/time
=(2–1)/(t-0)
1 represents the position at which the particle is moving about a fixed axis, at time 0, and 2 represents the position at time t. Here d=(2–1),dt=(t-0)
dw= d/dt
The angular velocity is equal to dw/dt
=d/dt(d/dt)
= d2/dt2
Their units also differ. The units of acceleration are rad/second2 for angular and m/s2 for centripetal.
Find angular velocity from centripetal speed
The formula to calculate centripetal speed is
a= v2/r
We know now that the linear velocity (v) and the angular speed (w) are related by the relationship v=wr, where r represents the radius of the route. This relationship can be used to determine that a=(w.r.2)2/r
= w2.r2/r
= w2.r
We can determine the angular speed if we have the values for the radius and centripetal velocity. We know the angular velocity is equal to dw/dt.
We can therefore calculate the angular speed from the calculated value for angular velocity, and the time value that was provided.
Relationship Between Angular and Centripetal Acceleration
The relationship between angular acceleration and centripetal acceleration can be understood by examining their connection to each other and their influence on the motion of objects.
Angular acceleration refers to the rate at which the angular velocity of an object changes over time. Angular velocity, on the other hand, is the rate of change of angular displacement. It measures the speed at which an object rotates or revolves.
Centripetal acceleration, on the other hand, is the acceleration experienced by an object moving in a circular path. It is directed towards the center of the circle and allows the object to continuously change its direction while maintaining a constant speed.
The connection between angular acceleration and centripetal acceleration can be described using the concept of linear or tangential acceleration. Linear acceleration represents the change in the linear velocity of an object moving along a curved path. Angular acceleration is related to linear acceleration through the equation:
Angular Acceleration (α) = Linear Acceleration (a) / Radius (r)
This equation shows that angular acceleration is inversely proportional to the radius of the circular path. In other words, as the radius decreases, the angular acceleration increases, and vice versa. This relationship indicates that objects moving in smaller circles experience higher angular acceleration than those moving in larger circles.
Conversely, to convert between angular and linear acceleration, we can use the equation:
Linear Acceleration (a) = Angular Acceleration (α) * Radius (r)
This equation allows us to relate the rotational motion of an object to its linear motion. It shows that the linear acceleration experienced by an object depends on the angular acceleration and the radius of the circular path.
By understanding the relationship between angular acceleration and centripetal acceleration, we can gain insights into the dynamics of objects in circular motion. These concepts are essential for analyzing and predicting the behavior of rotating objects and their interaction with their surroundings.
Angular acceleration and centripetal acceleration are interconnected through their relationship with linear acceleration and the radius of the circular path. This relationship helps us understand the motion of objects in circular paths and their acceleration patterns.
Applications of Angular and Centripetal Acceleration
Examples in Physics
Angular and centripetal acceleration play crucial roles in various phenomena observed in physics. For example, when a car takes a turn at high speed, centripetal acceleration keeps it moving in a curved path. Similarly, the rotation of planets around the sun can be explained using these concepts.
Practical Applications
Apart from theoretical applications, angular and centripetal acceleration find practical uses in everyday life. They are essential in designing amusement park rides, such as Ferris wheels or roller coasters, which rely on circular motion. Additionally, engineers utilize these principles when designing and analyzing rotating machineries, such as turbines or motors.
Conclusion
The Difference Between Angular Acceleration and Centripetal Acceleration lies in their definitions, purposes, and applications. Angular acceleration deals with the rate of change of rotational speed, while centripetal acceleration describes the inward acceleration in circular motion. Understanding these concepts is vital for grasping rotational and circular dynamics in various fields, from engineering to astronomy. By knowing their differences and applications, scientists and engineers can better design and analyze systems involving circular motion, leading to technological advancements and discoveries that shape our world.